座標系の姿勢（回転）の表現

直交行列で述べたように座標系の姿勢の表現と 座標系の姿勢やベクトルの回転変換は基本的に同じものである． ここでは様々な姿勢（回転）の表現について説明する．

図1 座標系の姿勢(回転)の表現

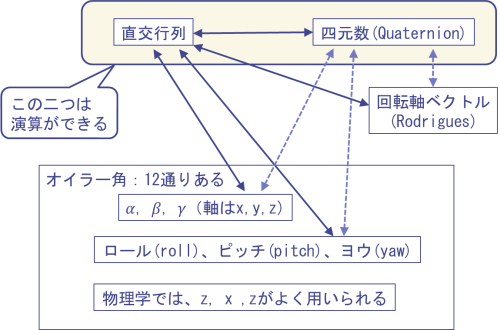
図1に代表的な座標系の姿勢の表現方法の相互の関係を簡単に示す． 直交行列と四元数による表現は演算が可能である．

四元数による表現は直交行列とくらべてデータ数が少なく一軸周りの回転を 素直に表せる， オイラー角などの表現と比べてジンバルロックを起こさないなどの理由で 最近はよく用いられている． しかし座標系の座標軸の取り出しなどは簡単ではないため，ロボットの動作表現を 考えたときにはあまり直感的ではないし，演算が軽いとも言えないと思う．

ここでは直交行列による表現を中心にそれぞれの表現の関係を説明する．

まず座標軸周りの回転を考える．

図3 x軸周りの回転

図3はx軸周りに$ \theta $回転したものである． このとき， $$ \boldsymbol{e}_x = \left( \begin{array}{c} 1 \\ 0 \\ 0 \end{array} \right), \: \boldsymbol{e}_y = \left( \begin{array}{c} 0 \\ \cos \theta \\ \sin \theta \end{array} \right), \: \boldsymbol{e}_z = \left( \begin{array}{c} 0 \\ - \sin \theta \\ \cos \theta \end{array} \right) $$

となっていることはすぐ分かる．

すなわちx軸周りに$ \theta $回転する直交行列$R_x (\theta) $は以下になる． $$ R_x (\theta) = \left( \begin{array}{c} \boldsymbol{e}_x & \boldsymbol{e}_y & \boldsymbol{e}_z \end{array} \right) = \left( \begin{array}{cc} 1 & 0 & 0 \\ 0 & \cos \theta & - \sin \theta \\ 0 & \sin \theta & \cos \theta \end{array} \right) \tag{1} $$

同様 ¹⁾ にy, z軸周りの回転を表す直交行列は以下のようになる．

$$ R_y (\theta) = \left( \begin{array}{cc} \cos \theta & 0 & \sin \theta \\ 0 & 1 & 0 \\ - \sin \theta & 0 & \cos \theta \end{array} \right) \tag{2} $$ $$ R_z (\theta) = \left( \begin{array}{cc} \cos \theta & -\sin \theta & 0 \\ \sin \theta & \cos \theta & 0 \\ 0 & 0 & 1 \end{array} \right) \tag{3} $$

座標軸周りの3つの回転角度による姿勢表現をオイラー角という． レオンハルト・オイラー²⁾により 考案されたもので，連続する2つの軸が異なっていれば良いので，12通りの組み合わせがある． 単に「オイラー角」と言った場合に分野によって異なるものを指していることが多いので注意が必要である．

ロボットの分野では$\alpha$,$\beta$,$\gamma$とロール，ピッチ，ヨー（roll, pitch, yaw (rpy)）の表現がよく用いられる． この２つは異なる3つの軸周りの回転で姿勢を表現するものであり本質的には同じものである．

図3 roll. pitch, yaw

ロール，ピッチ，ヨーは乗り物の姿勢を表現するときに用いられるもので，乗り物の前方向と進行方向のズレをヨー角， 前方向と水平面との角度をピッチ角，前方向周りのねじれ角をロール角と呼ぶ． 進行方向をx軸，鉛直方向をz軸にとることが多い．x軸周りの回転がロール，z軸周りの回転がヨーである． この場合，y軸周りの回転がピッチ角になるが下向きにダイブする向きが正方向となる． 航空機の場合はz軸を鉛直下向きに取ることでヘッドアップが正方向となるようにすることも多い． ロボットの分野では進行方向をz軸，グリッパの開き方向をy軸に取ることも多い． その場合，x軸周りがヨー，y軸周りがピッチ，z軸周りがロールとなる． このどちらであるかは定めがないので注意が必要である．

ロボットの分野での$\alpha$,$\beta$,$\gamma$の表現は x軸周りが$\alpha$でヨー角，y軸周りが$\beta$でピッチ角，z軸周りが$\gamma$でロール角となっている ³⁾． この$\alpha$,$\beta$,$\gamma$の方が座標軸のとり方にも呼び方にも紛れがなくおすすめである． またロボットが上からものを掴むときを考えると，鉛直方向とグリッパの進行方向（もしくはその逆方向）が 一致しているという点でも理解しやすい． ただし$\alpha$,$\beta$,$\gamma$はヨー，ピッチ，ロールの順になっていることには注意が必要である．

ヨー，ピッチ，ロール（$\alpha$,$\beta$,$\gamma$）は人間にとって直感的に姿勢を理解しやすいという 利点があるが，問題点もいくつかある ⁴⁾．

図4 ヨー，ピッチ，ロール表現の問題点

具体的には，図4の

• ピッチ（$\beta$）が$ \pm{\pi/2}$になるとヨー（$\alpha$），ロール（$\gamma$）の区別がつかなくなる（この状態は，特異点であり，３軸の回転機構の状態になぞらえてジンバルロックなどとも呼ばれている）．
• ヨー，ロールが$\pm{\pi}$を，ピッチが$\pm{\pi/2}$を超えると表現が一つに定まらなくなる．周期性があり範囲を限ると切り替えのときに不連続が生じる．

図4以外でも，

• 直接演算ができない．たとえば2組のロール，ピッチ，ヨー表現のそれぞれの要素の加算は姿勢の変換として意味をなさない．
• パラメタ空間が均質ではない．イメージとしては地球の経度，緯度（ヨー，ピッチに相当）を考えると極点に経度線が集まる．

などがある．

図5 $\alpha$,$\beta$,$\gamma$の表現

$\alpha$,$\beta$,$\gamma$の表現では，まずx軸の周りに$\alpha$回転させ，次に回転した後の y軸（図のy'）の周りに$\beta$回転させ，最後に回転した後のz軸（$\boldsymbol{e}_z$）周りに$\gamma$回転させる．

これは直交行列の積として順次右から掛けていけば良い．すなわち $$ R_x(\alpha)R_y(\beta)R_z(\gamma) = \left( \begin{array}{cc} 1 & 0 & 0 \\ 0 & \mathrm{cos}\, \alpha & - \mathrm{sin}\, \alpha \\ 0 & \mathrm{sin}\, \alpha & \mathrm{cos}\, \alpha \end{array} \right) \left( \begin{array}{cc} \mathrm{cos}\, \beta & 0 & \mathrm{sin}\, \beta \\ 0 & 1 & 0 \\ - \mathrm{sin}\, \beta & 0 & \mathrm{cos}\, \beta \end{array} \right) \left( \begin{array}{cc} \mathrm{cos}\, \gamma & - \mathrm{sin}\, \gamma & 0 \\ \mathrm{sin}\, \gamma & \mathrm{cos}\, \gamma & 0 \\ 0 & 0 & 1 \end{array} \right) $$ $$ = \left( \begin{array}{cc} \mathrm{c}(\beta) \mathrm{c}(\gamma) & - \mathrm{c}(\beta) \mathrm{s}(\gamma) & \mathrm{s}(\beta) \\ \mathrm{s}(\alpha) \mathrm{s}(\beta) \mathrm{c}(\gamma)+\mathrm{c}(\alpha) \mathrm{s}(\gamma) & - \mathrm{s}(\alpha) \mathrm{s}(\beta) \mathrm{s}(\gamma)+\mathrm{c}(\alpha) \mathrm{c}(\gamma) & - \mathrm{s}(\alpha) \mathrm{c}(\beta) \\ - \mathrm{c}(\alpha) \mathrm{s}(\beta) \mathrm{c}(\gamma)+\mathrm{s}(\alpha) \mathrm{s}(\gamma) & \mathrm{c}(\alpha) \mathrm{s}(\beta) \mathrm{s}(\gamma)+\mathrm{s}(\alpha) \mathrm{c}(\gamma) & \mathrm{c}(\alpha) \mathrm{c}(\beta) \end{array} \right) \tag{4} $$

ちなみに，z軸周りをヨー，y軸周りをピッチ，x軸周りをロールとしたときの直交行列は以下のようになる．

$$ R_z(y)R_y(p)R_x(r) = \left( \begin{array}{cc} \mathrm{cos}\, y & - \mathrm{sin}\, y & 0 \\ \mathrm{sin}\, y & \mathrm{cos}\, y & 0 \\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{cc} \mathrm{cos}\, p & 0 & \mathrm{sin}\, p \\ 0 & 1 & 0 \\ - \mathrm{sin}\, p & 0 & \mathrm{cos}\, p \end{array} \right) \left( \begin{array}{cc} 1 & 0 & 0 \\ 0 & \mathrm{cos}\, r & - \mathrm{sin}\, r \\ 0 & \mathrm{sin}\, r & \mathrm{cos}\, r \end{array} \right) \\ $$ $$ = \left( \begin{array}{cc} \mathrm{c}(y) \mathrm{c}(p) & - \mathrm{s}(y) \mathrm{c}(r) + \mathrm{c}(y) \mathrm{s}(p) \mathrm{s}(r) & \mathrm{s}(y) \mathrm{s}(r) + \mathrm{c}(y) \mathrm{s}(p) \mathrm{c}(r) \\ \mathrm{s}(y) \mathrm{c}(p) & \mathrm{c}(y) \mathrm{c}(r) + \mathrm{s}(y) \mathrm{s}(p) \mathrm{s}(r) & - \mathrm{c}(y) \mathrm{s}(r) + \mathrm{s}(y) \mathrm{s}(p) \mathrm{c}(r) \\ - \mathrm{s}(p) & \mathrm{c}(p) \mathrm{s}(r) & \mathrm{c}(p) \mathrm{c}(r) \end{array} \right) \tag{5} $$

逆に直交行列$A$が与えられたときに，その$\alpha$,$\beta$,$\gamma$を求める．

$$ A = \left( \begin{array}{c} \boldsymbol{a}_x & \boldsymbol{a}_y & \boldsymbol{a}_z \end{array} \right) = \left( \begin{array}{cc} a_{xx} & a_{yx} & a_{zx} \\ a_{xy} & a_{yy} & a_{zy} \\ a_{xz} & a_{yz} & a_{zz} \end{array} \right) \tag{6} $$ この行列表現は少し注意が必要である．$a_{ij}$は$\boldsymbol{a}_i$の$j$成分，すなわち$ij$が「行，列」ではなく「列，行」の順になっている ⁵⁾

このとき $$ - \pi/2 \le \beta \le \pi/2　\\ - \pi \lt \alpha \le \pi \\ - \pi \lt \gamma \le \pi $$ の制約をつける．

式(4)と式(6)の係数を比較すると $$ a_{zx} = \mathrm{sin}\, \beta \\ \therefore \; \beta = \mathrm{sin}^{-1}(a_{zx}) $$ $ - \pi/2 \lt \beta \lt \pi/2 $ のとき， $$ 0 \lt \mathrm{cos}\, \beta \le 1 $$ よって $$ \alpha = \mathrm{atan2}(- a_{zy}, a_{zz}) \\ \gamma = \mathrm{atan2}(- a_{yx}, a_{xx}) $$ ここで$\mathrm{atan2}$は$(- \pi , \pi ]$の値域で象限を考慮した角度を返す関数である．

$\beta=\pi/2$のとき，式(4)にこれを代入し，三角関数の加法定理を用いて式を整理する． $$ \left( \begin{array}{cc} 0 & 0 & 1 \\ \mathrm{s}(\alpha) \mathrm{c}(\gamma)+\mathrm{c}(\alpha) \mathrm{s}(\gamma) & - \mathrm{s}(\alpha) \mathrm{s}(\gamma)+\mathrm{c}(\alpha) \mathrm{c}(\gamma) & 0 \\ - \mathrm{c}(\alpha) \mathrm{c}(\gamma)+\mathrm{s}(\alpha) \mathrm{s}(\gamma) & \mathrm{c}(\alpha) \mathrm{s}(\gamma)+\mathrm{s}(\alpha) \mathrm{c}(\gamma) & 0 \end{array} \right) $$ $$ = \left( \begin{array}{cc} 0 & 0 & 1 \\ \mathrm{sin}(\alpha + \gamma) & \mathrm{cos}(\alpha + \gamma) & 0 \\ - \mathrm{cos}(\alpha + \gamma) & \mathrm{sin}(\alpha + \gamma) & 0 \end{array} \right) \tag{7} $$ 式(7)と式(6)の係数を比較すると， $$ \alpha+\gamma=atan2(a_{xy}, a_{yy}) $$ これ見て分かるように$\alpha$と$\gamma$は分離することができない． 便宜的には$\alpha = 0$として解を求めることが多い． $\beta=-\pi/2$のときも同様に式(4)に代入して，三角関数の加法定理で整理する． $$ \left( \begin{array}{cc} 0 & 0 & -1 \\ - \mathrm{sin}(\alpha - \gamma) & \mathrm{cos}(\alpha - \gamma) & 0 \\ \mathrm{cos}(\alpha - \gamma) & \mathrm{sin}(\alpha - \gamma) & 0 \end{array} \right) \tag{8} $$ $$ \alpha-\gamma=atan2(-a_{xy}, a_{yy}) $$

同様に式(5)と式(6)の係数を比較すると,

$$ p = - \mathrm{sin}^{-1}(a_{xz}) $$ $ - \pi/2 \lt p \lt \pi/2 $ のとき， $$ y = \mathrm{atan2}(a_{xy}, a_{xx}) \\ r = \mathrm{atan2}(a_{yz}, a_{zz}) $$ $\beta=\pi/2$のとき， $$ \left( \begin{array}{cc} 0 & - \mathrm{s}(y) \mathrm{c}(r) + \mathrm{c}(y) \mathrm{s}(r) & \mathrm{s}(y) \mathrm{s}(r) + \mathrm{c}(y) \mathrm{c}(r) \\ 0 & \mathrm{c}(y) \mathrm{c}(r) + \mathrm{s}(y) \mathrm{s}(r) & - \mathrm{c}(y) \mathrm{s}(r) + \mathrm{s}(y) \mathrm{c}(r) \\ - 1 & 0 & 0 \end{array} \right) = \left( \begin{array}{cc} 0 & - \mathrm{sin}(y-r) & \mathrm{cos}(y - r) \\ 0 & \mathrm{cos}(y-r) & \mathrm{sin}(y - r) \\ - 1 & 0 & 0 \end{array} \right) $$ $$ y-r = atan2(-a_{yx},a_{zx}) $$ $\beta=-\pi/2$のとき， $$ \left( \begin{array}{cc} 0 & - \mathrm{s}(y) \mathrm{c}(r) - \mathrm{c}(y) \mathrm{s}(r) & \mathrm{s}(y) \mathrm{s}(r) - \mathrm{c}(y) \mathrm{c}(r) \\ 0 & \mathrm{c}(y) \mathrm{c}(r) - \mathrm{s}(y) \mathrm{s}(r) & - \mathrm{c}(y) \mathrm{s}(r) - \mathrm{s}(y) \mathrm{c}(r) \\ 1 & 0 & 0 \end{array} \right) = \left( \begin{array}{cc} 0 & - \mathrm{sin}(y+r) & - \mathrm{cos}(y + r) \\ 0 & \mathrm{cos}(y+r) & - \mathrm{sin}(y + r) \\ 1 & 0 & 0 \end{array} \right) $$ $$ y+r = atan2(-a_{yx},-a_{zx}) $$

異なる２つの座標系間の回転変換は一つの回転軸とその周りの回転角度で表現することができる．

この表現の利点は，

• 一回の回転で実現できる

ということであり，回転軸が一定のきれいな動作でロボットの手先の姿勢を変更するなどに使える. $\alpha$,$\beta$,$\gamma$などの表現ではそれらを同時になめらかに動かしたとしてもきれいな回転にはならない．

また欠点は，

• 人間には回転軸が座標系の軸と異なるので直感的に分かりにくいことが多いこと
• 0（回転軸が存在しない）と$\pi$（回転角の最大を$\pi$に制約しても2方向から回せる）が特異点になること

である．

回転行列から回転軸と回転角度を求めるのは次節に譲る． ここでは 任意の回転軸$\boldsymbol{n}$の周りに$\theta$回転したときに 座標系がどのような姿勢になるか（すなわちその回転行列）を求める．

これには座標軸がどのように変化するかを考えればよい． まずx軸について考える． ここで $$ \boldsymbol{x} = \left( \begin{array}{c} 1 \\ 0 \\ 0 \end{array} \right) \; , \; \boldsymbol{n} = \left( \begin{array}{c} n_x \\ n_y \\ n_z \end{array} \right) $$ である．$\boldsymbol{n}$は正規化されているとする⁶⁾．

図6 x軸の回転

図6のように$\boldsymbol{x}$を$\boldsymbol{n}$に垂直なベクトル$\boldsymbol{r}$と 平行なベクトル$\boldsymbol{d}$に分解する．

$$ \boldsymbol{x}=\boldsymbol{r}+\boldsymbol{d} $$ ここで， $$ \boldsymbol{d}=(\boldsymbol{x} \cdot \boldsymbol{n}) \, \boldsymbol{n} = n_x \boldsymbol{n} \\ \boldsymbol{r}= \boldsymbol{x} - \boldsymbol{d} = \boldsymbol{x} - n_x \boldsymbol{n} $$ $\boldsymbol{r}$を回転したベクトルを${\boldsymbol{r}'}$とすると $$ \boldsymbol{e}_x = \boldsymbol{r}' + \boldsymbol{d} $$

図7 r'の分解

ここで図7のように$\boldsymbol{r}'$を$\boldsymbol{r}$と $\boldsymbol{n} \times \boldsymbol{r}$で分解する． $$ \boldsymbol{r}' = \boldsymbol{r}\,\mathrm{cos}\,\theta + (\boldsymbol{n} \times \boldsymbol{r})\,\mathrm{sin}\,\theta $$ ここで $$ \boldsymbol{n} \times \boldsymbol{r} = \boldsymbol{n} \times (\boldsymbol{x} - n_x \boldsymbol{n}) = \boldsymbol{n} \times \boldsymbol{x} $$ よって $$ \boldsymbol{e}_x=\boldsymbol{r}' + \boldsymbol{d} = n_x \boldsymbol{n} + (\boldsymbol{x} - n_x \boldsymbol{n} )\,\mathrm{cos}\,\theta + (\boldsymbol{n} \times \boldsymbol{x})\,\mathrm{sin}\,\theta $$ これを成分表示して計算すると ^{7) 8)}， $$ \boldsymbol{e}_x = n_x \left( \begin{array}{c} n_x \\ n_y \\ n_z \end{array} \right) + \left\{ \left( \begin{array}{c} 1 \\ 0 \\ 0 \end{array} \right) - n_x \left( \begin{array}{c} n_x \\ n_y \\ n_z \end{array} \right) \right\} \mathrm{cos}\, \theta + \left( \begin{array}{c} 0 \\ n_z \\ - n_y \end{array} \right) \mathrm{sin}\, \theta $$ 整理して， $$ \boldsymbol{e}_x = \left( \begin{array}{c} \mathrm{cos}\,\theta + n_x^2 (1 - \mathrm{cos}\,\theta) \\ n_x n_y (1 - \mathrm{cos}\,\theta) + n_z \mathrm{sin}\,\theta \\ n_z n_x (1 - \mathrm{cos}\,\theta) - n_y \mathrm{sin}\,\theta \end{array} \right) $$ 同様に⁹⁾， $$ \boldsymbol{e}_y = \left( \begin{array}{c} n_x n_y (1 - \mathrm{cos}\,\theta) - n_z \mathrm{sin}\,\theta \\ \mathrm{cos}\,\theta + n_y^2 (1 - \mathrm{cos}\,\theta) \\ n_y n_z (1 - \mathrm{cos}\,\theta) + n_x \mathrm{sin}\,\theta \end{array} \right) $$ $$ \boldsymbol{e}_z = \left( \begin{array}{c} n_z n_x (1 - \mathrm{cos}\,\theta) + n_y \mathrm{sin}\,\theta \\ n_y n_z (1 - \mathrm{cos}\,\theta) - n_x \mathrm{sin}\,\theta \\ \mathrm{cos}\,\theta + n_z^2 (1 - \mathrm{cos}\,\theta) \end{array} \right) $$ これをまとめると， $$ R(\boldsymbol{n}, \theta) $$ $$ = \left( \begin{array}{cc} \mathrm{cos}\,\theta + n_x^2 (1 - \mathrm{cos}\,\theta) & n_x n_y (1 - \mathrm{cos}\,\theta) - n_z \mathrm{sin}\,\theta & n_z n_x (1 - \mathrm{cos}\,\theta) + n_y \mathrm{sin}\,\theta \\ n_x n_y (1 - \mathrm{cos}\,\theta) + n_z \mathrm{sin}\,\theta & \mathrm{cos}\,\theta + n_y^2 (1 - \mathrm{cos}\,\theta) & n_y n_z (1 - \mathrm{cos}\,\theta) - n_x \mathrm{sin}\,\theta \\ n_z n_x (1 - \mathrm{cos}\,\theta) - n_y \mathrm{sin}\,\theta & n_y n_z (1 - \mathrm{cos}\,\theta) + n_x \mathrm{sin}\,\theta & \mathrm{cos}\,\theta + n_z^2 (1 - \mathrm{cos}\,\theta) \tag{9} \end{array} \right) $$

直交行列から回転軸，回転角度を求める場合は回転角度を正，すなわち$[0,\pi]$に制限する必要がある． 回転角度を負にすることとベクトルを符号反転（逆向き）にすることは同じであり一意に定めることができなくなるからである．

式(6)と式(9)の係数を比較する．

$$ \begin{eqnarray} a_{xx} + a_{yy} + a_{zz} &=& \mathrm{cos}\,\theta + n_x^2 (1 - \mathrm{cos}\,\theta) + \mathrm{cos}\,\theta + n_y^2 (1 - \mathrm{cos}\,\theta) + \mathrm{cos}\,\theta + n_z^2 (1 - \mathrm{cos}\,\theta) \\ &=& 3 \mathrm{cos}\,\theta + (n_x^2 + n_y^2 + n_z^2)(1 - \mathrm{cos}\,\theta) \\ &=& 1 + 2 \mathrm{cos}\,\theta \end{eqnarray} $$ よって $$ \mathrm{cos}\,\theta = (a_{xx} + a_{yy} + a_{zz} - 1)/2 $$ $$ \theta = \mathrm{cos}^{-1}((a_{xx} + a_{yy} + a_{zz} - 1)/2), \; 0 \le \theta \le \pi $$ また $$ \begin{eqnarray} a_{yz} - a_{zy} &=& (n_y n_z (1 - \mathrm{cos}\,\theta) + n_x \mathrm{sin}\,\theta ) - (n_y n_z (1 - \mathrm{cos}\,\theta) - n_x \mathrm{sin}\,\theta) \\ &=& 2 n_x \mathrm{sin}\,\theta \end{eqnarray} $$ よって,$\mathrm{sin}\,\theta \ne 0$（すなわち$\theta \ne 0$ and $\theta \ne \pi）$の場合， $$ n_x = (a_{yz} - a_{zy} ) / (2\,\mathrm{sin}\,\theta) $$ 同様に $$ n_y = (a_{zx} - a_{xz} ) / (2\,\mathrm{sin}\,\theta) $$ $$ n_z = (a_{xy} - a_{yx} ) / (2\,\mathrm{sin}\,\theta) $$ $ \theta = 0 $の場合は，無回転なので回転軸は存在しない． 一方，$\theta = \pi$の場合は，式(9)に代入して， $$ \left( \begin{array}{cc} -1 + 2 n_x^2 & 2 n_x n_y & 2 n_z n_x \\ 2 n_x n_y & -1 + 2 n_y^2 & 2 n_y n_z \\ 2 n_z n_x & 2 n_y n_z & -1 + 2 n_z^2 \end{array} \right) $$ 係数を比較すると $$ -1 + 2 n_x^2 = a_{xx} $$ $$ -1 + 2 n_y^2 = a_{yy} $$ $$ -1 + 2 n_z^2 = a_{zz} $$ $$ 2 n_x n_y = a_{xy} = a_{yx} $$ $$ 2 n_y n_z = a_{yz} = a_{zy} $$ $$ 2 n_z n_x = a_{zx} = a_{xz} $$ よって $$ n_x = \pm \sqrt{{1 + a_{xx}} \over 2} $$ $ n_x \ne 0 $の場合，$\pi$回転はどちらに回しても同じなので正負はどちらを選んでもよい． 他の成分はこれと整合を取るため以下のように計算する． $$ n_y = a_{xy}/ 2 n_x $$ $$ n_z = a_{zx}/ 2 n_x $$ $ n_x = 0 $の場合は他の成分から解けば良い．

ここの説明では$ n_x $から解いたが実際には上３つの式を解いて 一番絶対値の大きい成分から残りを計算すると精度的にも良い値が得られる．