逆運動学を用いた動作の注意点

文書の過去の版を表示しています。

動作の目標がハンドなどがとるべき座標系（位置・姿勢）として与えられた場合，一般には逆運動学計算で関節パラメタ（関節角度）を求めて動作させることが多い ¹⁾．

その場合，以下の点に注意する必要がある．

複数損愛する逆運動学解のどれを選択するか
始点と終点を関節角で補間してしまうと中間点が想定と異なることがある
関節角の可動範囲，制限を考慮して逆運動学を選択する必要がある

これらについて一つずつ検討する．

簡単のため平面２関節のアームを考えてみる．

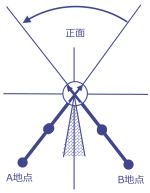
たとえば図1のようにロボットの正面（第一関節がゼロ度のときの方向）左側にあるA地点では点線より実線の解を採用したくなるかもしれない ²⁾．そのようにした場合逆に正面右側にあるB地点では対称性を考えて実線の解を採用するのは自然なことである．

しかし，その選択に基づいてA地点からB地点への連続した動作を行った場合，図2のようにアームは一旦真っ直ぐに伸びた特異姿勢を通過することになる．

これに対してB地点での買い手して点線のものを採用した場合には図3のように特異姿勢を通過しない比較的素直な動作となる．

図2と図3の違いはあまり大きくないようにも見えるが，図4のように始点と終点が近い場合はより際立つことになる．

図1 逆運動学解の選択

図2 特異姿勢を通過する動作

図3 特異姿勢を通過する動作

図4 始点と終点が近い場合

これれは次節で述べるように始点から終点への軌道を分割してのぞみの軌道を生成しようとした場合にはとりわけ大きな問題となる．

解を正しく選択すればこの問題を避けることは可能であるが，複数ある解のどれとどれを採用すればよいのかその選択は簡単ではない．

たとえば3自由度アームの位置決めでも4通りの解があり，6自由度アームで位置・姿勢を制御する場合には8通りの解がある．

図5 軌道の分割

一般に逆運動学計算で始点と終点の関節パラメタを求めて動作させても，関節パラメタで補間して動作させるとその軌道は図5のように必ずしも直線にはならない．

直線に限らず，手先の軌道を希望通りのものにしようとするならば軌道を十分に細かく分割してそれぞれの分割点での逆運動学解を求め, それをつないでいく必要がある．

このような場合には特に前節で述べた解の選択が重要となる．途中で解の選択を誤れば手先の軌道は前節の図4のようにその瞬間に大きく異なる軌道を通過することになる．

ここで述べたのぞみの軌道の生成や前述解の選択の問題は，始点を初期解とした逆運動学の数値解法や分解運動制御を用いることで比較的素直に解決することができる．

これは逐次的な解法が特異姿勢を乗り越えることが出来ないという欠点を逆にうまく利用していることになっている．

アームの可動域の問題は前述の2つとはまた異なる視点の問題となる．一般に逆運動学解を求めるときには関節の可動域を考慮しないことが多い．もちろん実際問題としては解を求めた後に可動域内かどうかをチェックする．しかし，始点と終点がともに可動域内にあったとしても，軌道の途中が可動域内かどうかは保証がない．

例として３自由度アームの逆運動学で扱ったアームをを考えてみよう．図6,7は，それを上から見たものである．「正面」というのはアームのx軸方向であり$\theta_1 = 0$のときの第１リンクのx軸方向と一致している．図の中心にある円内の矢印は第１リンクのx軸方向を示している．逆運動学解を求めるときは可動範囲を考慮していなかったが，たとえば図6のようにでアームの根本の回転軸（$\theta_1$）の可動範囲が ±170°，すなわち後ろ側20°の範囲は通過できないとする ³⁾．このような制約は実際のアームとしてはありふれたものである．

図6ではA地点，B地点の逆運動学解として$\theta_1$に対して３自由度アームの逆運動学の式(4)，すなわち第１リンクのx軸方向にアームを向けた素直な解を採用している．この解を用いた場合には図6のように大回りをすることになる ⁴⁾．

しかし３自由度アームの逆運動学の式(10)，すなわち，根本の回転軸を前に向けたまま後ろにアームを回す姿勢を用いた場合には，図7のように始点から終点へと無駄なく移動することができる．

解の選択という意味では，図6のA地点から図7のb地点への移動というイメージしにくい軌道を考えることもできる．