三次元直交行列（回転行列）と座標系

ロボットの分野では直交行列は大きく以下の３つの役割を果たす．

• 直交座標系（ひいては物体）の姿勢を表現する
• 参照座標系を替えた場合のベクトルの成分表示の変換を行う
• 直交座標系やベクトルの回転変換を行う

直交行列とは以下を満たす行列のことである． $$ A^\mathrm{T} A = A A^\mathrm{T} = I $$ ここで$ I $は単位行列， $$ I = \left( \begin{array}{cc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} \right) $$ である． これは $$ A^{-1}=A^\mathrm{T} $$ ということであり，行列$ A $の転置行列$ A^\mathrm{T}$が逆行列$A^{-1}$になっていることがわかる．

ここで$ A $を以下のように3つの縦ベクトルで表現すると， $$ A= \left( \begin{array}{c} \boldsymbol{e}_x & \boldsymbol{e}_y & \boldsymbol{e}_z \end{array} \right)　\tag{1} $$ $$ A^\mathrm{T} A = \left( \begin{array}{c} \boldsymbol{e}^\mathrm{T}_x \\ \boldsymbol{e}^\mathrm{T}_y \\ \boldsymbol{e}^\mathrm{T}_z \end{array} \right)\left( \begin{array}{c} \boldsymbol{e}_x & \boldsymbol{e}_y & \boldsymbol{e}_z \end{array} \right) =\left( \begin{array}{cc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} \right) $$

図1 直交座標系

すなわち $$ \begin{array}{cc} \boldsymbol{e}_x \cdot \boldsymbol{e}_x = 1 & \boldsymbol{e}_y \cdot \boldsymbol{e}_y = 1 & \boldsymbol{e}_z \cdot \boldsymbol{e}_z = 1 \\ \boldsymbol{e}_x \cdot \boldsymbol{e}_y = 0 & \boldsymbol{e}_y \cdot \boldsymbol{e}_z = 0 & \boldsymbol{e}_z \cdot \boldsymbol{e}_x = 0 \end{array} $$ であり，$ \boldsymbol{e}_x $, $ \boldsymbol{e}_y $, $ \boldsymbol{e}_z $ は正規直交基底となっている． つまり直交行列は三次元直交座標系の座標軸を並べたものであり，これを用いて座標系の姿勢を表現することができる¹⁾．

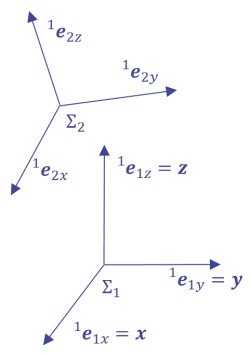
ここで注意しなくてはいけないのは直交行列は成分表示されなくてはならないということである． 三次元ベクトルで述べているように，成分表示するためには参照座標系を決める必要がある． たとえば図1のように参照座標系を座標系$ \Sigma_1 $とするなら座標系$ \Sigma_2 $を表す直交行列は $$ ^1A_2 = \left( \begin{array}{c} ^1\boldsymbol{e}_{2x} & ^1\boldsymbol{e}_{2y} & ^1\boldsymbol{e}_{2z} \end{array} \right) $$ となる．

ちなみに座標系$ \Sigma_1 $自身を表す直交行列は当然ながら $$ ^1A_1 = \left( \begin{array}{c} ^1\boldsymbol{e}_{1x} & ^1\boldsymbol{e}_{1y} & ^1\boldsymbol{e}_{1z} \end{array} \right) =\left( \begin{array}{cc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} \right) = I $$ となる．

図2 参照座標系の変換

ベクトルの成分表示が複数の座標系間でどのように変換されるか考える． 三次元ベクトルの式(8)を示す． $$ {^1v_x} ^i\boldsymbol{e}_{1x} + {^1v_y} ^i\boldsymbol{e}_{1y} + {^1v_z} ^i\boldsymbol{e}_{1z} = {^2v_x} ^i\boldsymbol{e}_{2x} + {^2v_y} ^i\boldsymbol{e}_{2y} + {^2v_z} ^i\boldsymbol{e}_{2z} $$

これを行列とベクトルの積の形で整理すると， $$ {^iA_1} {^1\boldsymbol{v}} = {^iA_2} {^2\boldsymbol{v}} $$ ここで$ i = 1 $すると， $$ ^1\boldsymbol{v} = {^1A_1} {^1\boldsymbol{v}} = {^1A_2} {^2\boldsymbol{v}} \tag{2} $$ 式(2)は座標系$ \Sigma_1 $で成分表示された座標系$ \Sigma_2 $の直交行列をベクトルの座標系$ \Sigma_2 $での成分表示にかけることで座標系$ \Sigma_1$での成分表示に変換されることを示している．

同様に，座標系$ \Sigma_0 $で成分表示された座標系$ \Sigma_1 $の直交行列をベクトルの座標系$ \Sigma_1 $での成分表示にかけることで座標系$ \Sigma_0$での成分表示に変換することができる． $$ ^0\boldsymbol{v} = {^0A_1} {^1\boldsymbol{v}} \tag{3} $$

図3 直交行列の積の連鎖

また式(2)と式(3)から $$ ^0\boldsymbol{v} = {^0A_1}{^1A_2}{^2\boldsymbol{v}} \tag{4} $$ となることが分かる．これはまた $$ ^0A_2 = {^0A_1}{^1A_2} \tag{5} $$ であることを示している． このように参照座標系によるベクトルの成分表示の変換や直交行列による座標系の姿勢表現は直交行列の積の形で 連鎖させて計算できることが分かる（図3）．

図4 直交行列の表記の工夫

このときベクトルや直交行列の参照座標系を示す左上の添字と その参照行列を表現する直交行列の右下の添字が一致し，打ち消し合うように見えるように添字が工夫されている（図4）．

また式(2)に左から$ ^2A_1 $をかけると， $$ ^2\boldsymbol{v} = {^2A_1} {^1\boldsymbol{v}} = {^2A_1} {^1A_2} {^2\boldsymbol{v}} $$ であり， $$ ^2A_1 = {^1A_2^{-1}} = {^1A_2^\mathrm{T}} \tag{6} $$ であることが確認できる．

直交行列は，一つには座標系の姿勢を表すと解釈することもできるが， 座標系の姿勢変換（回転）を表していると解釈することもできる．

式(5)は，参照座標系を連鎖させてその表現を計算しているわけだが， 見方によっては元の座標系の姿勢を直交行列で（回転）変換させて 希望する姿勢の座標系の直交行列を計算するのにも使える．

上記の座標系に対する回転変換は比較的理解しやすいと思う．

一方，ベクトルに対する回転変換は理解のためにもう少し説明が必要になる． 式(3)は，参照座標系を替えたときの同じベクトルの成分表示を計算しているわけだが， 逆に，同じ座標系の違うベクトルの成分表示だとしたら２つのベクトルの関係はどうなるだろうか．

図5 直交行列によるベクトルの回転

式(3)のままでは少し理解しにくいので以下のように少し書き換えてみる（図5）． $$ ^0\boldsymbol{v}^{\prime} = {^0A_1}{^1\boldsymbol{v}^{\prime}} = {^0A_1}{^0\boldsymbol{v}} \tag{7} $$ ここで$ ^0\boldsymbol{v}^{\prime} $ と ${^1\boldsymbol{v}^{\prime}} $ は同じベクトルを異なる参照座標系で成分表示したもので，${^1\boldsymbol{v}^{\prime}} $と$ {^0\boldsymbol{v}}$ は同じ成分表示だが異なる座標系のベクトルである． ${^1\boldsymbol{v}^{\prime}} $と$ {^0\boldsymbol{v}}$ の関係をよく考えてみると$ {^0\boldsymbol{v}}$を${^0A_1}$で座標系ごと姿勢を変化させたものが${^1\boldsymbol{v}^{\prime}} $になっている． つまり${^1\boldsymbol{v}^{\prime}} $と$ {^0\boldsymbol{v}}$ の関係，すなわち${^0\boldsymbol{v}^{\prime}} $と$ {^0\boldsymbol{v}}$ の関係は${^0A_1}$で姿勢変換（回転変換）したものになっている．

座標系を設定せずに回転変換のみに注目して表現する場合は,同じ直交行列ではあるが $$^0A_1$$ などの表記ではなく $$R$$ と表記して区別することも多い．