逆運動学（幾何的/解析的手法）

逆運動学とは，順運動学とは逆に手先の位置・姿勢が与えられたときに，それを実現する関節パラメタを求める問題である． 逆運動学の問題は以下のようにいろいろと難しい点がある．

• 解がないことがある（可動範囲外）
• 解が複数個存在することがある
• 解が無限に存在することがある（特異姿勢，冗長自由度）
• 幾何的/解析的手法では解くことが難しいことが多い．

まずは3自由度アーム，6自由度アームの幾何的/解析的手法での解を求める．

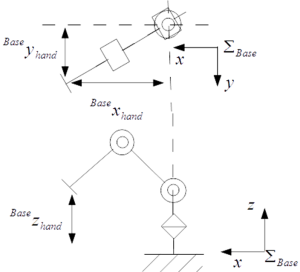
まずは３自由度アームの順運動学で用いた図1のアームの逆運動学を扱う． 3自由度アームは可動範囲内の任意の位置に移動することができる． そのためさらに多自由度のアームの場合も，これをベースにして位置と姿勢を分離して 逆運動学を解くことが多い．

図1 3自由度アーム

図2 3自由度アームの逆運動学

図2のように手先位置， $$ \left( \begin{array}{c} ^0x_{wrist} \\ ^0y_{wrist} \\ ^0z_wrist \end{array} \right) $$ が与えられたときの関節角度,$\theta_1$,$\theta_2$,$\theta_3$を求める問題である．

順運動学の式は， $$ {^0x_{wrist}} =　{^1x_{wrist}}\mathrm{cos}\,\theta_1 = (l_2 \mathrm{sin}\, \theta_2 + l_3 \mathrm{sin}(\theta_2 + \theta_3))\mathrm{cos}\,\theta_1 \tag{1} $$ $$ {^0y_{wrist}} = {^1x_{wrist}}\mathrm{sin}\,\theta_1 = (l_2 \mathrm{sin}\, \theta_2 + l_3 \mathrm{sin}(\theta_2 + \theta_3))\mathrm{sin}\,\theta_1 \tag{2} $$ $$ ^0z_{wrist} = l_b+l_1+l_2 \mathrm{cos}\, \theta_2 + l_3 \mathrm{cos}(\theta_2 + \theta_3) \tag{3} $$ 図2の上図と式(1)と式(2)より，${^0x_{wrist}} ={^0y_{wrist}} = 0$でなければ， $$ \theta_1 = \mathrm{atan2}({^0y_{wrist}},\,{^0x_{wrist}})　\tag{4} $$ となる¹⁾． ただし，$\theta_1$をこのようにすると$^1x_{wrist}$は必ず正になる．$\theta_1$を反対側（$\pi$回した側）にした解も存在するのでそれについては後で求める．

図3 リンク1の座標系のxz平面

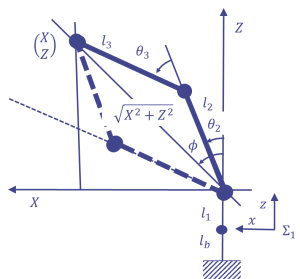
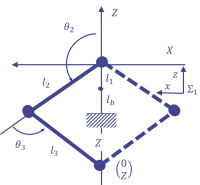
ここで図3のようにリンク1の座標系のxz平面を考える．さらにリンク2の原点の高さを減じたあらたなXZ座標を導入する． $X$,$Z$は与えられた手先位置とリンクの長さを使ってい以下のように表せる．上で述べたように$X={^1x_{wrist}}>0$である． よって， $$ X = \sqrt{{^0x_{wrist}^2} + {^0y_{wrist}^2}} \tag{5} $$ $Z$は高さ分差し引いて， $$ Z = {^0z_{wrist}} - l_b - l_1 \tag{6} $$ となる．ちなみにこの$Z$はリンク2の原点位置になっている．

ここで$l_2$,$l_3$,$\sqrt{X^2+Z^2}$の三角形に着目すると，その角度は余弦定理で求めることができる ²⁾. $\theta_3$に着目すると，

$$ X^2+Z^2=l_2^2+l_3^3-2l_2l_3\mathrm{cos}(\pi-\theta_3)=l_2^2+l_3^3+2l_2l_3\mathrm{cos}\theta_3 $$ $$ \mathrm{cos}\theta_3 = {{X^2+Z^2-l_2^2-l_3^2} \over {2l_2l_3}}　\tag{7} $$ よって， $$ \theta_3 = \pm\mathrm{cos}^{-1}\left({{X^2+Z^2-l_2^2-l_3^2} \over {2l_2l_3}}\right) \tag{8} $$ 正の値が実線，負の値は点線の三角形になる．

ここで$\phi$を求めると， $$ \phi = \mathrm{atan2}\left({X ,\; Z}\right) \tag{9} $$ であり,

$\theta_2$に関して余弦定理を使うと $$ l_3^2 = X^2+Z^2+l_2^2 - 2l_2\sqrt{(X^2+Z^2)}\,\mathrm{cos}(\phi - \theta_2) $$ よって， $$ \phi - \theta_2 = \pm\mathrm{cos}^{-1} \left( {X^2+Z^2+l_2^2-l_3^2} \over {2l_2\sqrt{(X^2+Z^2)}}\right) $$ $$ \theta_2 = \mathrm{atan2}\left({X ,\; Z}\right) \mp\mathrm{cos}^{-1} \left( {X^2+Z^2+l_2^2-l_3^2} \over {2l_2\sqrt{(X^2+Z^2)}}\right) \tag{10} $$ $\theta_2$は$\mp$の正の側が点線の三角形になる．

図4 $\theta_1$を反対側（$\pi$回した側）にした解

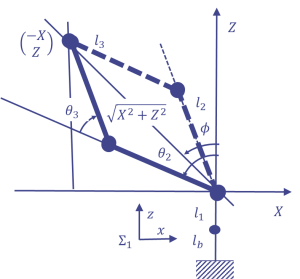
つぎに図4の$\theta_1$を反対側（$\pi$回した側）にした解を考える．これは， $$ \theta_1 = \mathrm{atan2}(-{^0y_{wrist}},\,-{^0x_{wrist}})　\tag{11} $$ とすることになる．

このとき図4のように手先はX軸の負の側になる．そこで式(5)の$X$はそのまま使うこととして手先位置を $\left( \begin{array}{c} -X \\ Z \end{array} \right)$ とする．

$\theta_3$に着目すると，式(8)は変更なしで大丈夫だが，形は同じでもY軸が紙面向こう側になるので 正の値の実線が図3とは逆になる．

また$\phi<0$となるが，$\mathrm{atan2}$を使うので $$ \phi = \mathrm{atan2}\left({-X ,\; Z}\right) \tag{11} $$ とすれば正しく求められる．

$\theta_2<0$であるので，式(11)の$\phi$から余弦定理で得られた$\mathrm{cos}^{-1}$を引けば実線に対する $\theta_2$が正しく求められるので，ここは式(10)の$\phi$の部分を式(11)で置き換えて， $$ \theta_2 = \mathrm{atan2}\left({-X ,\; Z}\right) \mp\mathrm{cos}^{-1} \left( {X^2+Z^2+l_2^2-l_3^2} \over {2l_2\sqrt{(X^2+Z^2)}}\right) $$ となる．

図5 $X=0$$Z>0$の場合

図6 $X=0$,$Z<0$の場合

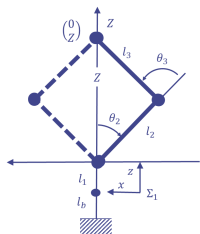
さらに図5，図6の${^0x_{wrist}} ={^0y_{wrist}} = 0$すなわち式(5)の$X=0$の場合を考える． 図5は$Z>0$で，図6は$Z<0$である．

このとき$\theta_1$は不定（どの値でもOK）になる ³⁾.

$\theta_3$は，式(8)で$X=0$としたものと同じになる． ただし，値が正のときに対応する姿勢は図5，図6に示す実線になる．

$\theta_2$については， 図5の$X>$の場合 $\phi=0$でありこれについては式(8),$\theta_2$については式(10)で$X=0$としたものと同じになる．

図6の$Z<0$の場合$\phi=\pi$であり式(8)で$X=0$としたものと同じになる． $\theta_2$についても，実線の姿勢はそこから余弦定理で求めた内角を減じたものになっているので， これも式(10)で整合が取れている．

最後に$X=0$，$Z=0$を考える．

$l_2=l_3$の構造のアームでなければ取りえない姿勢となる．

その場合，$\theta_1$は不定となり，$\theta_3=\pi$となる． また$\phi$も不定となるため$\theta_2$も不定になる．

これらは式(8),(9),(10)で$X=0$，$Z=0$として得られる結果と同じである．

解の存在範囲は式(7)から以下のように制限される． $$ 1 \ge \mathrm{cos}\, \theta_2 \ge -1 $$ すなわち $$ (l_2+l_3)^2 \ge X^2+Z^2 \ge (l_2-l_3)^2 $$ これは，$\Sigma_1$の原点を中心とした半径$l_2+l_3$の球の内側で半径$|l_2-l_3|$の球の外側の範囲である．

等号の場合，すなわちそれぞれの球面上であり，それぞれ腕が伸び切った状態（$\theta_2=0$），縮みきった状態（$\theta_2=\pi/2$）となっている． この場合は，

手先位置， $$ \left( \begin{array}{c} ^0x_{wrist} \\ ^0y_{wrist} \\ ^0z_wrist \end{array} \right) $$ が与えられたとき，まず， $$ X = \sqrt{{^0x_{wrist}^2} + {^0y_{wrist}^2}} $$ $$ Z = {^0z_{wrist}} - l_b - l_1 $$ を計算する．

$X \ne 0$の一般姿勢の場合， $$ \theta_1 = \mathrm{atan2}({^0y_{wrist}},\,{^0x_{wrist}}) $$ に対して， $$ \theta_3 = \pm\mathrm{cos}^{-1}\left({{X^2+Z^2-l_2^2-l_3^2} \over {2l_2l_3}}\right) $$ $$ \theta_2 = \mathrm{atan2}\left({X ,\; Z}\right) \mp\mathrm{cos}^{-1} \left( {X^2+Z^2+l_2^2-l_3^2} \over {2l_2\sqrt{(X^2+Z^2)}}\right) $$ の2つの解が得られる．また， $$ \theta_1 = \mathrm{atan2}(-{^0y_{wrist}},\,-{^0x_{wrist}}) $$ に対して， $$ \theta_3 = \pm\mathrm{cos}^{-1}\left({{X^2+Z^2-l_2^2-l_3^2} \over {2l_2l_3}}\right) $$ $$ \theta_2 = \mathrm{atan2}\left({-X ,\; Z}\right) \mp\mathrm{cos}^{-1} \left( {X^2+Z^2+l_2^2-l_3^2} \over {2l_2\sqrt{(X^2+Z^2)}}\right) $$ の2つの解が得られ，合計4つの解が存在する．
ただし，$\theta_3$が$0$もしくは$\pi$になる場合はそれぞれアームが伸びきった状態，縮みきった状態となり2つの解が1つに縮退し， 解の数が合計2つとなる特異姿勢になっている．

$X=0$,$Z\ne0$の場合， $\theta_1$は不定となり， $$ \theta_3 = \pm\mathrm{cos}^{-1}\left({{Z^2-l_2^2-l_3^2} \over {2l_2l_3}}\right) $$ $$ \theta_2 = \mathrm{atan2}\left({0 ,\; Z}\right) \mp\mathrm{cos}^{-1} \left( {Z^2+l_2^2-l_3^2} \over {2l_2\sqrt{(Z^2)}}\right) $$ 上記の$\theta_2$に関する式はさらに簡略化できるが場合分けが増えるのでここで止めておく．

$X=0$,$Z=0$の場合，$l_2=l_3$の構造のアームでなければ解はない．解がある場合は， $\theta_1$と$\theta_2$は不定となり，$\theta_3=\pi$となる．

いずれの場合も，$\mathrm{cos}^{-1}$の引数が$[-1,1]$の範囲でなければ解が存在しない． これは三角不等式（縮退した等号部分も含む）の条件になっている．

具体的には，解が存在するのはリンク2の原点を中心として， 半径$(l_2-l_3)^2$の球の外側で半径$(l_2+l_3)^2$の球の内側の領域となる ^{4) 5)}．

比較的簡単そうに見える3自由度アームの逆運動学だが，完全に解ききるのは結構大変である．

私自身，特に実線と点線の姿勢の切り替わりがむずかしく， 限定された領域でのみ正しく区別できているが解く範囲を広げると思っていたのと逆になるという解を用いていて 解の選択に際して混乱することもあった．

たとえば，$^0x_{wrist}$が正から負へ変わるような動作を作る時に図3の状態から図4の状態の実線の 姿勢を求めれば姿勢を大きく変えることなく動作するが，それぞれで図3の実線の解を使うとロボットの 姿勢が大きく変化してしまう．

このように解が複数存在するため，解の選択を誤ると手先の位置はほとんど変わらないのにアームの姿勢が大きく変化するということが起きるので解の選択には注意が必要である．

この辺に関しては逆運動学を用いた動作の注意点でもう少し詳しく説明する．

６自由度アームの順運動学で用いた図7のアームの逆運動学について考える．

図7　6自由度アーム

図8 手順の概略

このアームのベースからハンドまでの順運動学は， $$ ^0T_{hand}(\theta_1,\,\theta_2,\,\theta_3,\,\theta_4,\,\theta_5,\,\theta_6) ={^0T_1(\theta_1)}{^1T_2(\theta_2)}{^2T_3(\theta_3)}{^3T_4(\theta_4)}{^4T_5(\theta_5)}{^5T_6(\theta_6)}{^6T_{wrist}}{^{wrist}T_{hand}} \tag{12} $$ である．6自由度アームでは，位置だけでなく姿勢も，すなわちハンドなどの手先の座標系を決めることができる．

逆運動学問題は$^0T_{hand}$が与えられたとき， それを実現する$\theta_i,\,(i = 1..6)$を求める問題である．

$\theta_i$に依存しない部分の除いて以下の形に書き換えておく． $$ ^0T_6={^0T_{hand}}{^{wrist}T_{hand}^{-1}}{^6T_{wrist}^{-1}}　= {^0T_6}(\theta_1,\,\theta_2,\,\theta_3,\,\theta_4,\,\theta_5,\,\theta_6) \tag{13} $$

このアームの構造は図8のように第4,5,6関節の軸が1点（リンク5の原点）に集まっており，位置と姿勢をその点で分離して解くことが出来る． 解き方の概要は以下のようになる．

1. 先端座標（リンク6）が指定されると，リンク5の原点置が決まる（図9）
2. リンク4の回転はリンク3からリンク5原点までの距離に影響しないので，リンク5の原点は，$\theta_1,\,\theta_2,\,\theta_3$の3自由度アームの求め方で解くことができる（図10）
3. リンク3までの座標変換が決まれば残りの3自由度は姿勢の調整で比較的簡単に決まる（図11）

図9 リンク5の原点

図10 3自由度アーム

図11 姿勢の決定

各ステップをもう少し詳しく説明する．

式(13)から目標手先座標が与えられるとリンク6が決まる．このとき図9に示すように リンク6の原点からリンク6のz軸方向に$l_5$だけ戻してやることでリンク5の原点が定まる．

リンク5の原点はリンク3のz軸方向に$l_3+l_4$の位置にあるのでリンク3の長さをその分伸ばした形で，リンク5の原点位置を目標とした$\theta_1,\,\theta_2,\,\theta_3$の3自由度アームの逆運動学を解けば それらを決定できる⁶⁾．

$\theta_1,\,\theta_2,\,\theta_3$が決まると，順運動学計算によりリンク3の座標系が決定できる．

リンク3の座標系が決まると図11から分かるように座標系の姿勢を追うことで$\theta_5,\,\theta_4,\,\theta_6$が決定される．

リンク3のz軸（＝リンク4のz軸）とリンク6のz軸に垂直な方向がリンク5のy軸となる．それらの方向の差がリンク5のy軸周りの回転角度$\theta_5$となる ⁷⁾． リンク5のy軸は一般には相対する2方向があるので，それに応じて$\theta_5$も2通りの解が存在する． それぞれのz軸が同一方向もしくは反対方向⁸⁾は特異姿勢で $\theta_5=0$または$\theta_5=\pi$となる. その場合リンク5のy軸は不定，すなわちリンク4とリンク5のz軸周りの回転角度が分離できず個々には不定となる．

リンク5のy軸とリンク4のy軸は同じ方向であり，それとリンク3のy軸との角度の差が$\theta_4$となる．

リンク6のy軸とリンク5のy軸との角度の差が$\theta_6$となる．

一般の姿勢では$\theta_4,\,\theta_5\,\theta_6$の解は$\theta_5$の向きに応じて2通り存在する． $\theta_1,\,\theta_2,\,\theta_3$が4通りなので組み合わせで8通りの解が存在することになる．

以上が6自由度アームの逆運動学の解法になる．一応アルゴリズムとしては理解できると思うが， これを数式として展開するには，補助変数を導入し，ベクトルの演算，座標変換を駆使するなどを行う必要があり とても難しい．実際にはプログラムとして実装する方が簡単である．

ここでは3自由度と6自由度アームの逆運動学を幾何的／解析的に解く方法を示した．

これらを解くにはかなりの幾何学的な直感が要求される．頭の体操としてはとても興味深いものがある．

しかしロボットの動作制御などでの実用性を考えた場合，いくつかの問題点もある．

• 複数解の選択が難しい
• 解法が複雑でプログラムの実装に苦労する
• 複雑な構造のアームへの対応はさらに困難を伴う
• 冗長自由度など選択できる解が無限にある場合の対応がアドホックになる
• 冗長自由度の有効利用が難しい

これらに対する一つの答えは逆運動学の数値解法である． これは基本的に多変数非線形方程式の数値解法である． 逆運動学の数値解法では一階偏微分係数行列（ヤコビ行列）を利用した ニュートンラフソン法について説明する．